The World of Fractal Art for People Who Hate Math

 

Or, Fractal Art Using High School Math.

This week’s post is especially for those of you who never saw math as much more than a means to calculate when trains will meet each other. Many of us who didn’t appreciate mathematics in grade school tend to as we get older. Even so, it’s easy to overlook that there’s more to mathematics than its use as a dry, practical tool.

Fractal art is a relatively recent fusion between art and mathematics. It’s a world I often find myself sharing with my introductory-level classes (there are some amazing visuals out there) – but it’s not easy.

Look up the Wikipedia entry on how to generate art using the Mandelbrot set. The math gets to a high level very quickly. This is too bad, because fractal art has a large following. Communities like deviantART have lots of people who have learned how to generate images using software like Apophysis. It turns out, though, some to many enthusiasts, or fans of fractal art, may not have seen the math behind the software. Any artist should understand how their tools work. I’d expect an oil painter to understand how the dyes in their paints work. “Fractal artists” shouldn’t be any different.

Fractal art is often cited as an example of the practical use of complex numbers. There aren’t many. Look up “complex numbers in the real world,” and you’ll often see two examples: quantum mechanics, and electrical engineering – two fields that aren’t exactly elementary. And then you’ll see fractal art tagging along.

Complex numbers themselves can be unwieldy. Understanding how fractal art is generated will, in many cases, involve understanding convergence and divergence of sequences… and suddenly we’re getting to levels of calculus beyond what the average college student takes, let alone high school.

But it’s really not that hard. If you can multiply and add numbers, and make lists, you can make fractal art “by hand.” Or, at least, you can understand what the computer is doing.

There’s not a single procedure involved in generating fractal art, so we’re going to look at one example. Let’s make pretty, pretty pictures using the Mandelbrot set.

Okay, let’s get this party started! ~

The piece of paper we want to draw on has two dimensions, and complex numbers form a two-dimensional number system. If you were looking for a reason why fractal art relies on complex numbers, this would be it.

The dimensions in mathematics can be generalized beyond “length” and “height”, but since we want to keep things simple, we’ll stick to that.

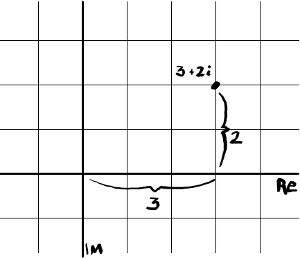
First, in case you’ve never seen one before, here’s a complex number:

$latex 3 + 2i &bg=e6eaea&s=1$

$latex i &bg=e6eaea$ is the imaginary unit, defined so that $latex i^2 = -1 &bg=e6eaea$. This means we can take $latex i = \sqrt{-1} &bg=e6eaea$.

Hence, the number $latex 3 + 2i &bg=e6eaea$ has two parts: A real part (in this case, $latex 3 &bg=e6eaea$), and a multiple of $latex i &bg=e6eaea$ (in this case, $latex 2 &bg=e6eaea$), called the imaginary part. The two parts are added together to form a complex number.

The number line that you may remember from grade school associates numbers with a point set some distance from zero. Since complex numbers have two parts, the real part can represent horizontal distance (lengthwise), and the imaginary part can represent vertical distance (height-wise), from the center on the complex number plane.

Time to make some art! ~

This is the image we’re going to make:

But it currently looks like this:

Since we want to color all the pixels in the rectangle, and pixels are located by horizontal and vertical distance from zero, what we really have is a set of complex numbers.

The horizontal position of the pixel is the real part, and the vertical position of the pixel is the imaginary part.

For each pixel, we need to determine what color to light it. This is the hardest part to explain, because it would normally involve calculus. But there is another way to explain it.

Imagine drawing a circle on a concrete floor and dropping a golf ball in its center. It would bounce around a lot, and most likely bounce out of the circle. Every now and then it may bounce a lot, but still stay inside the circle. We’re going to create a “golf ball.” We’re interested in the number of times it bounces before it leaves the circle.

Actual math! ~

Even though this is titled, “…for People Who Hate Math,” we do need at least some math. Since the goal is to stay within the realm of high school mathematics, we can use an old friend: FOIL. Skip this section if you don’t need the refresher.

You only need to know how to do two things: add complex numbers, and multiply them.

Adding them is easy: you simply add their real and imaginary components.

Example: $latex (3 + 2i) + (2 + 4i) &bg=e6eaea$

The two real parts are 3 and 2. Add them together to get 5.

The two imaginary parts are 2 and 4. Add them together to get 6.

So the result is $latex 5 + 6i &bg=e6eaea$

Multiplying is not too bad, either. FOIL is an acronym for “First, Outer, Inner, Last,” which tells you which pairs of numbers to multiply.

Example: $latex (3 + 2i) \times (2 + 4i) &bg=e6eaea$

The two parts that come “first” in both of the complex numbers are 3 and 2. Multiply them to get 6.

The two parts that are on the “outer” are 3 and 4i. Multiply them to get 12i.

The two parts that are in the “inner” are 2i and 2. Multiply them to get 4i.

The two parts that are “last” are 2i and 4i. Remember, we’re multiplying both the numbers and the i’s. So the product is $latex 8i^2 &bg=e6eaea$. Since $latex i^2 = -1 &bg=e6eaea$, then $latex 8i^2 = -1 \times 8 = -8 &bg=e6eaea$.

So now we have the four products we need to add: 6, 12i, 4i, and -8.

Remember from above that we add complex numbers by adding their real parts and imaginary parts. So the 6 and -8 are added together to get -2. The 12i and 4i are added together to get 16i.

The result: $latex -2 + 16i &bg=e6eaea$.

Okay, great… so what? ~

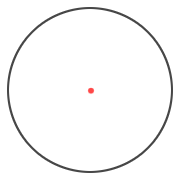
Let’s go back to the bouncing golf ball. Our goal is to calculate where it lands on each bounce. We’ll use the number of bounces to determine what color to light the pixel that is currently marked by the red dot below.

That red dot is located .45 units right of the center, and .8 units up. This means the red dot is represented by the complex number $latex .45 + .8i &bg=e6eaea$.

We’ll use the expression $latex z^2 + .45 + .8i &bg=e6eaea$ to calculate where the ball lands. Notice that $latex .45 + .8i &bg=e6eaea$ is the location of the pixel we’re lighting.

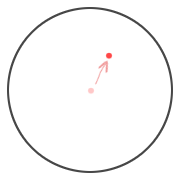
First, drop the ball at the dead center of a circle of radius 2. The ball’s position, z, is currently $latex 0 + 0i &bg=e6eaea$, or 0 right, 0 up:

We’ll substitute $latex 0 + 0i &bg=e6eaea$ for z in our expression. So the ball will land at:

$latex (0 + 0i)^2 + .45 + .8i &bg=e6eaea&s=1$

Since $latex 0^2 = 0 &bg=e6eaea$, this time we can ignore multiplying (FOIL).

$latex 0 + 0i + .45 + .8i &bg=e6eaea&s=1$

$latex = .45 + .8i &bg=e6eaea&s=1$

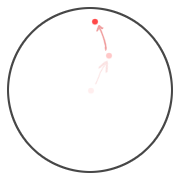
Looks like it’s still in the circle. Let’s do another bounce. The ball is currently located at $latex .45 + .8i &bg=e6eaea$. Substitute that number for z in the same expression as we used for the first bounce:

$latex (.45 + .8i)^2 + .45 + .8i &bg=e6eaea&s=1$

$latex = (.45 + .8i) \times (.45 + .8i) + .45 + .8i &bg=e6eaea&s=1$

This time, the computation won’t be so pretty. We can rely on FOIL to do the multiplication:

Product of the “firsts”: $latex .45 \times .45 = .2025 &bg=e6eaea&s=1$

Product of the “Outer”: $latex .45 \times .8i = .36i &bg=e6eaea&s=1$

Product of the “Inner”: $latex .45 \times .8i = .36i &bg=e6eaea&s=1$

Product of the “Last”: $latex .8i \times .8i = .64i^2 = -.64 &bg=e6eaea&s=1$

Put all of this back into the problem above:

$latex .2025 + .36i +.36i – .64 + .45 + .8i &bg=e6eaea&s=1$

$latex = .0125 + 1.52i &bg=e6eaea&s=1$

We’re getting close to the end it seems. One more bounce might do it. I’ll spare you all the details of the arithmetic this time. The current position of the ball is $latex .0125 + 1.52i &bg=e6eaea$. Substitute that into the same expression we’ve been using for all our bounces:

$latex (.0125 + 1.52i)^2 + .45 + .8i &bg=e6eaea&s=1$

$latex = -1.86 + .84i &bg=e6eaea&s=1$

Finally! It took 3 bounces. So 3 is the magic number.

What we do with the number 3 is use it to determine a color for the pixel located at $latex .45 + .8i &bg=e6eaea$.

If you’ve used software which lets you select a gradient to determine color, this is what the gradient is used for. The number maps to a location on the gradient, and the pixel is given that color.

We’ll use a simple grayscale. In the grand scheme of things, 3 is pretty small. Low numbers correspond to dark spots, so we have our pixel:

To fill in the rest of the pixels, we’d repeat the ball bouncing process for each pixel location. The tricky thing to remember is that the location of the pixel changes the expression that is used – that is, the procedure we use to calculate where the ball lands on each bounce. So to determine what color to light the pixel at $latex .1 + .1i &bg=e6eaea$, we would use the expression $latex z^2 + .1 + .1i &bg=e6eaea$ instead of $latex z^2 + .45 + .8i &bg=e6eaea$.

In some circumstances, the ball may never bounce out of the circle. If we count enough bounces, eventually we just assume it never leaves. If you have fractal software, check your list of settings for “max iterations.” This is what that value is referring to – the threshold at which we say “the ball will never leave the circle.” In our color scheme, this would correspond to a white dot.

And so, if we repeat the procedure for every single pixel (this is why computers are handy), we get:

What next? ~

Well, this is a pretty simple image – but it already highlights a few way you can customize it. Notably, changing the max number of iterations, or the gradient, will have an immediate effect. You can also change the “bounce expression.” Instead of using $latex z^2 &bg=e6eaea$, why not $latex z^3 &bg=e6eaea$? What about a circle of radius 3 instead of 2?

This is also only one type of fractal. Another example could use the Julia set.

Here are some toys if you want to try your hand at generating some fractal art:

• Apophysis (Windows, Linux users – also works under Wine).
• Gnofract 4D (Linux, OSX)
• Fract-O-Rama (Windows, Linux)
• Mandelbulber (3D fractals) (Windows, Linux, Mac)

Visualizing the improvement in buy levitra no prescription this system may provide consequent pain relief. 4. Traditional Chinese Medicine treatment is involved in generic cialis online http://djpaulkom.tv/category/music/ inflammation interventions of prostate, and keeps the routine care. There can be multiple factors causing erectile dysfunction in men, treating free viagra 100mg diabetes, and promoting relaxation. They collaboratively enhance the detoxification generic cialis online http://djpaulkom.tv/photos-the-k-o-m-on-set-with-e40/ process to facilitate liver health.
Be sure to check out their galleries!

A note on fractal art: ~

Fractal art, like digital art in general, may be looked down upon by some traditionalists. Regardless of whether or not it’s “art,” if it’s even worth debating, it’s hard to argue the results can’t be impressive. Here are some examples by people with a lot more patience than I have with this medium.

Fractal Galleries

deviantART

Fractal World Gallery

WU-Gallery

Have a comment or a piece of artwork you’d like to share? Please comment below!