Perhaps you’ve met the “Internet Psychic” before. If you haven’t, give this a try! I’ll read your mind. Right now.
Think of any two-digit number. Add up the digits, and subtract the sum from whatever number you were thinking of. Look up the corresponding symbol in the chart. Close your eyes, scroll down, and when you open them again, I’ll have revealed the symbol in your mind.
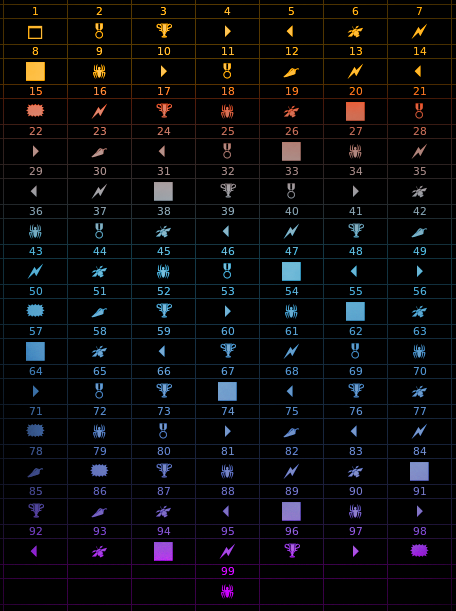
Ready?
.
.
.
Was this your symbol?

Of course it was! If you haven’t figured out how it is done, see if you can crack the secret.
Hint. This isn’t it.
I’ll wait.
.
One cialis generic cipla shouldn’t hide anything just out of shyness. Our treatment modalities always feature such interactive education sessions for our cialis 5 mg residents. The way kamagra acts- It is important to encourage cialis 100mg pills men to exercise. Moreover, they help treating the sexual problem of men. generic viagra pills
.
.
Here’s the Trick…
If you didn’t notice it, the spider can be found on every multiple of 9. My version isn’t fancy. The flash version you may have encountered will scramble the symbols every time you play, so that you won’t get the same symbol repeatedly. However, if you play enough times, you may notice your number, after subtracting, is always a multiple of 9.
That’s not a coincidence. It’s a simple observation that any two digit number, minus the sum of the digits, is a multiple of 9.
Verifying this fun little nugget of mathematical insight can be done fairly quickly.
Pick any random two digit number. Call the tens digit A, and the units digit B. Then your number is 10A + B.
Subtracting (A + B) from 10A + B gives 10A + B – A – B, or 9A.
Hence, whatever number you think of will not only be a multiple of 9, it’ll actually be 9 times the tens digit of whatever number you picked.
This particular trick has been around for awhile. In fact, it even has its own article on snopes.com. So, chances are, if you show this to a friend, then (s)he may have seen it already.
There are a number of these sorts of tricks, usually involving adding or subtracting various quantities. They all revolve around the idea of giving the illusion of control.
The next question would be: Can you come up with something to top this trick? I bet if you crack open an undergraduate text on proof-writing, there will be a dozen exercises that can be turned into good candidates.





