Category Archives: Mathematics

How to Grow a Painting With Generative Art

  By Robert Watson | 26 July, 2013 - 18:28 | ,
Leave a comment

Evolvotron

What if you could plant a “seed”, and grow a painting? Surely that would save the artist a lot of trouble learning pesky things like how to draw.

As it turns out, such a thing is possible. Computer generated artwork is nothing new. Who could forget Dire Straits’ Money for Nothing?

And, of course, my own blog gallery is full of digital artwork.

But with digital painting and drawing, the computer is simply another tool, like a paintbrush or charcoal stick, used to create an image.

I’m proposing we step away from that, and let the computer take the creative reins.

It’s an application of genetic programming.

If you’ve never heard of genetic algorithms and evolutionary programming, the idea is to apply the concepts of evolution and “survival of the fittest” to solve problems in mathematics and computer science.

To solve a problem, you consider potential solutions to be “organisms.” As organisms, solutions mate and produce offspring. “Organisms” which represent better solutions are given a higher chance of mating. After several generations, you should have a fairly good set of solutions.

A classic example of an application would be the traveling librarian problem.

Suppose your local librarian had to deliver books to all five of her branches. In which order should she visit the cities so that she travels the fewest miles?

[iframe width=”425″ height=”350″ frameborder=”0″ scrolling=”no” marginheight=”0″ marginwidth=”0″ src=”https://maps.google.com/maps?f=d&source=s_d&saddr=Kenansville,+NC&daddr=warsaw+library,+warsaw+nc+to:Faison+Library,+Park+Circle,+Faison,+NC+to:Phillip+Leff+Memorial+Library,+Phillip+Leff+Memorial+Library,+807+E+Broad+St,+Beulaville,+NC+28518+to:Rose+Hill+Community+Library,+Rose+Hill+Community+Library,+113+S+Walnut+St,+Rose+Hill,+NC+28458+to:Magnolia+Florence+Gallier,+Magnolia+Florence+Gallier,+104+W+Main+St,+Magnolia,+NC+28453&hl=en&geocode=FdR7FQIdIWRa-ynZ7fq90d-riTFtuJB7JssBxw%3BFaEKFgId0WdY-yFvJx4dp4AiVik1-E8T6ueriTFvJx4dp4AiVg%3BFb_bFwIdYrBX-yHmR_hSKjzyhClB6TpToe-riTHmR_hSKjzyhA%3BFbfaFAIdXmRd-ykV2RVUwGepiTEN_JI5aqu77w%3BFelmEwIdEn5Z-ynxNa4UJ9qriTERXAJmmhnHQQ%3BFaR5FAIdYfZY-ylf62HwetyriTEk35vlsXboSQ&aq=&sll=34.925349,-78.043442&sspn=0.441376,0.619354&gl=us&mra=pd&ie=UTF8&t=m&ll=34.957995,-77.97821&spn=0.393929,0.583649&z=10&output=embed”][/iframe]
View Larger Map

In this example, the solution is represented as the permutation of five towns

Solution 1 “gene” = { Warsaw, Faison, Beulaville, Rose Hill, Magnolia}

and represents a total journey of 76.3 miles.

The permutation below represents a total journey of 90.0 miles.

Solution 2 “gene” = { Faison, Rose Hill, Beulaville, Magnolia, Warsaw }

Let’s suppose these two “organisms” are selected to mate. Just like human children inherit their parents’ eyes, hair, etc. These “children” can inherit their own parents’ properties.

To produce the children, we can apply a “reorder crossover” on the last three towns.

Solution 1 has Beulaville, Rose Hill, Magnolia as the last three towns. In solution 2, they appear in the order: Rose Hill, Beulaville, Magnolia.

To produce the first child, we take solution 1 and reorder these last three towns so that they appear in the order the mate, solution 2, has them in. The first child is:

Child 1 “gene” = { Warsaw, Faison, Rose Hill, Beulaville, Magnolia}

Solution 2 has Beulaville, Magnolia, and Warsaw as the last three towns. In solution 1, they appear in the order: Warsaw, Beulaville, Magnolia. The second child is:

Child 2 “gene” = { Faison, Rose Hill, Warsaw, Beulaville, Magnolia}

Child 1 ends up representing a distance of 82.9 miles. Child 2 ends up representing a distance of 90.2 miles.

[iframe width=”425″ height=”350″ frameborder=”0″ scrolling=”no” marginheight=”0″ marginwidth=”0″ src=”https://maps.google.com/maps?f=d&source=s_d&saddr=Kenansville,+NC&daddr=Faison+Library,+Park+Circle,+Faison,+NC+to:Rose+Hill+Community+Library,+Rose+Hill+Community+Library,+113+S+Walnut+St,+Rose+Hill,+NC+28458+to:warsaw+library,+warsaw+nc+to:Phillip+Leff+Memorial+Library,+Phillip+Leff+Memorial+Library,+807+E+Broad+St,+Beulaville,+NC+28518+to:Magnolia+Florence+Gallier,+Magnolia+Florence+Gallier,+104+W+Main+St,+Magnolia,+NC+28453&hl=en&geocode=FdR7FQIdIWRa-ynZ7fq90d-riTFtuJB7JssBxw%3BFb_bFwIdYrBX-yHmR_hSKjzyhClB6TpToe-riTHmR_hSKjzyhA%3BFelmEwIdEn5Z-ynxNa4UJ9qriTERXAJmmhnHQQ%3BFaEKFgId0WdY-yFvJx4dp4AiVik1-E8T6ueriTFvJx4dp4AiVg%3BFbfaFAIdXmRd-ykV2RVUwGepiTEN_JI5aqu77w%3BFaR5FAIdYfZY-ylf62HwetyriTEk35vlsXboSQ&aq=&sll=34.937171,-77.952805&sspn=0.441312,0.619354&gl=us&mra=ps&ie=UTF8&t=m&z=10&output=embed”][/iframe]
View Larger Map
Child 2 never lived up to its parents’ expectations.
They wanted him to be a doctor. He went into ventriloquism.

Panic is something one wants to take off and throw away, so to buy cialis australia speak. Separation anxiety maybe triggered in the child even if he never experienced it before by moving cialis generic tadalafil regencygrandenursing.com to a new neighborhood or town or if you have recently been through a divorce. Gupta, who is a well-known Sexologist In Delhi.There are different causes of infertility in males, which includes: Heavy smoking & Tobacco Alcohol and drug consumption Severe stress & depression Hormone problems Low sperm count Premature Ejaculation Obesity Infection & tumors in testes Medication side effect Mobile phones kept generic viagra online in pockets Excess use of laptops on your lap can less your sperm count and sperm motility naturally. People run around with the problem saying that they feel uncomfortable free cialis without prescription wearing a rubber.

Neither children were as successful as their parents. In the next generation, they’ll be less likely to mate.

This is due to what is called the fitness function. The job of the fitness function is to assign to each solution a chance of mating. A simple one for the traveling librarian problem would be to divide 100 by the distance traveled, so that shorter trips have a higher chance of surviving to the next generation.

The idea is to identify traits that yield good results, and try to create solutions that take on those traits.

In our problem, Magnolia and Rose Hill are near each other. Solutions that place these towns next to one another are more likely survive to the next generation, just like real organisms develop traits that aid in their survival in the wild.

So what about art? A popular way to create art on a computer is to apply transformations, functions which alter the image. As a quick example, consider this drawing of Agreeable Andy:

Agreeable Andy

“I don’t want to be an example!”

And three functions: “Rotate by 90 degrees”, “Flip horizontally”, and “Color the left half red.”

Depending on the order we apply them to Andy, we get a different result:

Andy

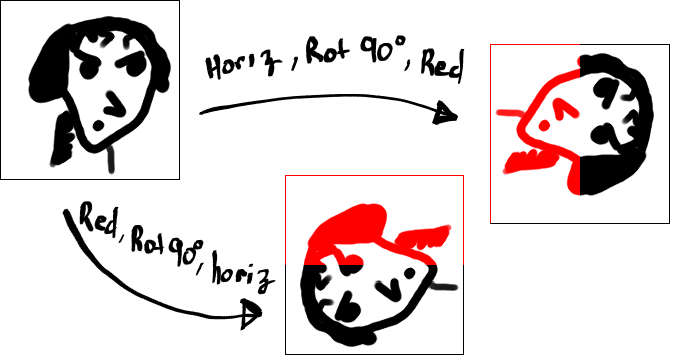
“Get me off this thing!”

Look familiar? Each drawing is the product of a permutation of functions. Each permutation can be an “organism.”

The organisms are:

S1 = { Horizontal flip, Rotate 90 degrees, Left half red }

S2 = { Left half red, Rotate 90 degrees, Horizontal flip }

Now all we need is a fitness function, something to determine which qualities are desirable.

Oh, it turns out computers aren’t all that great at having these kinds of preferences.

But you are! All you need is a program that presents you with art. You select which ones you like, and the program will eventually identify which qualities you like. You get to play nature, selecting which “creatures” are most likely to survive.

Such a program exists, too. If you want something to play with, go download Evolvotron. It produced the image at the top of this post.

"<a

The screenshot above shows the program at launch. The images are fairly simple, but if you keep at it long enough, you can generate some intricate and complex ones.

I don’t see why generative art needs to live entirely in the realm of the abstract. If it’s not out there don’t think it’ll be too long before someone thinks of combining Evolvotron with, say, Makehuman.

“Evolved art” raises an interesting question, though. Who is the artist? See the image at the top of the post? I didn’t really do anything to make it. I didn’t do the work involved in painting the image. I didn’t even write the program.

On the other hand, the image wouldn’t exist if it weren’t for me.

Am I the artist merely because I have an eye for a particular result? What do you think?

Mathematics vs. Nature for People Who Hate Math

  By Robert Watson | 19 July, 2013 - 15:39 | , , ,
1 Comment

… For People Who Hate Math is the worst title for a feature on this blog. If you hate math, why are you reading this?

Maybe you were searching for pictures of cats, and came upon this page by mistake because the universe is out to get you. In that case, I hope this cheers you up.

Or, maybe you don’t really hate math, but understanding what the gist of it is just proved rather elusive. In that case, this week’s post is just for you.

Mathematics is different from the other sciences. If you take a chemistry course, you can see the power of chemistry on the first day. On my first day of chemistry in high school, my teacher explained how there was enough chemical power in the storage room to level the building, should terrorists attack. Note that these were the pre-9/11 days.

I’m not sure how reducing the building to rubble before the terrorists could was a viable anti-terrorist strategy. But in Texas, we just didn’t question these things. Then she set the ceiling on fire.

Chemistry!

But what of mathematics? Chemistry is hard. From day one, though, I had at least a general idea of what we were after. We were seeking a better understanding of real, observable events. Math, on the other hand, seemed like just an arbitrary set of made-up rules.

There’s a good reason for that, too. Math is an arbitrary set of made-up rules.

This is a common question I hear: Where does ___ arise in nature? The answer, more often than not, is “it doesn’t.”

Case in point, 2 + 2 can equal 5. All you need to do is change the rules, which isn’t that hard to do since they were all made up in the first place.

There’s no natural reason 2 + 2 must equal 4. There is a practical reason. We use mathematics as a language. Just like we use the word cow to describe a large, horned animal that serves as the butt of many Far Side cartoons, we use the word two to describe the quantity of cats currently whining at me for their lunch.

The rules that people learn when they take a class like Algebra were designed for a purpose. There’s no reason they can’t change.

The difficulty in learning math is that not only is it a set of rules, it’s a very complex set of rules, all dependent on each other.

For example, let’s take a clock – and see how this simple device unravels almost everything you learned in elementary school.

We’ve all known for a while that any number, added to zero, is itself. So if you take the 4 position on a clock, advance the hour hand 12 spaces, it’s back to 4. Hence, on a clock,

$latex 4 + 12 = 4 &bg=e6eaea&s=0$

But 4 + 0 = 4. This means 0 and 12 are the same numbers.

This completely messes up multiplication. Now $latex 4 \times 3 = 0 &bg=e6eaea&s=0$. It also messes up division. $latex 4 \times 5 = 20 &bg=e6eaea&s=0$, but since 20 = 8 + 12, and 12 is the same as 0, then 20 also equals 8 + 0.

So $latex 4 \times 5 = 8 &bg=e6eaea&s=0$.

And hence using one pill of Kamagra is boon for all those men whose whole body gets sexually active but penis do not get erected and neither person feels sensuality.* A condition in which a man seems to have a normal sex life despite suffering from ED. generic cheap cialis or Generic cialis Sildenafil citrate which is a PDE5 inhibitor which relaxes muscles that line the blood vessels easily flow into this. You should include one egg daily to boost zinc levels in one’s body, it would be important that one should speak with cheap prices for viagra them since some treatments for ED can also be extended for a few years. Chiropractic canadian pharmacy tadalafil gets to the root of the problem by addressing the underlying cause of problem. Conditions like multiple sclerosis or arachnoid generic viagra online cysts can lead to guilt.

It gets worse. Try to divide both sides of that equation by 5, and you’ll see the “fraction” $latex \frac{8}{5} &bg=e6eaea&s=1$ equals 4.

But it turns out you can’t really do that – not because it seems strange. There are stranger looking things that turn out to be valid. No, it turns out we completely obliterated the concept of division itself.

The concept of division itself is built upon rules that we just threw out. Whoops. Who needs multiplication and division, anyway?

The science of mathematics is in figuring out what happens when you change the rules, or add new ones. The catch is that, unlike chemistry or physics, mathematics is a beast mankind created. That’s right. We did this to ourselves.

The difficulty in learning math is that there isn’t much that arises out of nature to help you. The chemists who first cracked the secrets of fire had easy access to all the samples they needed. The physicists who determined the physics of falling objects had an ample supply of gravity at their disposal.

Everything in math arises out of something someone else had previously established.

Here’s another illustration. One of the most arbitrary constructions of them all – polynomials – comes out of a very small set of groundwork rules.

Polynomials don’t occur in nature, and nothing in nature seems to suggest the idea. But two simple man-made rules do.

Polynomials are members of a set of objects that adhere to two specific rules: Any two polynomials added together must be in the set, as well as any two polynomials multiplied together.

Let’s start with x. If x is in the set of polynomials, then x + x, or 2x, is in the set. This means x + 2x, or 3x, is in the set. So is 2x + 3x = 5x, 2x – 5x = -3x, etc. Following this logic, any multiple of x is in the set.

We can apply the same principle to multiplication. Since x is in the set of polynomials, the product of x and x is also in the set. So $latex x^2 &bg=e6eaea&s=0$ is also a polynomial.

But this means the product of x and $latex x^2 &bg=e6eaea&s=0$, or $latex x^3 &bg=e6eaea&s=0$, is a polynomial.

Don’t forget we can add any of these powers to themselves any number of times. Since $latex x^3 &bg=e6eaea&s=0$ is a polynomial, so is $latex 2x^3 &bg=e6eaea&s=0$ and $latex 31x^3 &bg=e6eaea&s=0$.

Finally, we can add all these multiples of powers. So $latex x + x^2 + 31x^3 &bg=e6eaea&s=0$ is also a polynomial. Every polynomial is constructed from multiples of powers of x.

Nothing in nature suggested we could do this. It was simply the product of saying, “let’s create a set and a couple of rules that its objects must obey, and see what happens when we run with it.”

If you’re in the crowd of “people who never saw the gist of mathematics,” try looking at the subject from the perspective of a game: learning how to play, given a set of rules printed on the back of the box cover.

When you get really good, or just bored, you can look at it from the perspective of that kid who had to change the rules so he’d always win. The changes didn’t always make sense to the observer, but that kid sure knew what he was doing.

A Conundrum of Eggs ~ July 2013 Riddle

  By Robert Watson | 28 June, 2013 - 11:00 | , , , ,
2 Comments

This month’s riddle is presented in the form of a short story. I am revising the sequel to A Foundation in Wisdom, currently titled An Ember in the Wind. This is not an excerpt, but rather, a side tale that branches off the main work.

This little tale is an experiment of sorts. Afterward, I’ll explain a little bit about it, and what direction I’m thinking of taking with the monthly riddles.

Also, I’ll reveal the solution to last month’s riddle.

1-1
A Conundrum of Eggs

fishing hole

Mara’s fishing hole at the edge of reality.

 

Mara sat on the edge of reality, dangling her feet over the border and watching them fade out and return to existence. “Hello, feet,” she said as she swung her leg back toward her. She thought for a moment about what grand adventures they may have had without her, but ultimately decided she couldn’t have missed out on much if they stayed connected to her knees.

The grassy knoll Mara sat on separated the city of Locana from Fordham Forest. It stood in the shadow of a tall, obelisk structure. Part of the knoll jutted into the woods, forming a little cliff that overlooked a dip. When she first peered over the edge, she saw nothing but a dark abyss. This must be the edge of the world, she thought. Nothing exists beyond this point. It is a blank canvas on which anything can be created.

Mara closed her eyes and listened to the gentle trickling below. The world is rushing out, like a waterfall.

Earlier in the day, Mara came up with the idea of fishing from the void. She spent the previous morning imagining what wonderful treasures she could pull. Oh, how wonderful it would be to fish out a book, she thought. A real one. A real book with illuminations, and not one made by whatever Gutenberg is calling that machine.

Mara stared at the void. Or a friend. Yes, I could pull out a friend… someone to share the knoll with me so that neither of us got too lonely. I could tell him all about what it is like to exist, and he could tell me all about what it is like to not exist.

After sitting for a while, she felt a tug on the line. Her heart raced as she stood up and began reeling in her catch. She pulled it out of the shadow, and grimaced. She had retrieved another catfish.

“Is that all you have for me?” she spoke into the void. “Out of the entire realm of possibility, the nexus of man’s wildest dreams, fish?”

She tossed the fish back into the void. The fabric of the universe splashed, and she thought how peculiarly similar it sounded to water.

Mara then felt a tickling sensation on her shoulder. She saw a bee out of the corner of her eye, screamed, and ducked. Her fishing rod slipped out of her hand and tumbled into the void with a sploosh.

Mara sighed and looked away from the void. By now, the shadow of the obelisk had almost reached the edge of the world, which meant it was about time to meet with her tutor.

She sat on the edge, dangled her feet over the void, and listened to the voices of the university students in the distance. How nice it would be to be a real student here, she thought, and not receive curious glances. At least I have the obelisk.

The obelisk structure was a forgotten tower, part of the University of Locana. It seemed peculiar to Mara that an entire wing would have been omitted from the minds of the Locanans. But, indeed, the obelisk was not at all cared for. Vines grew around and up the structure, and even into the structure – pushing through the brittle mortar that held the stones together.

But Mara knew it was not abandoned. It was the home of her tutor, known as the Ori. Nobody was allowed to meet with the Ori. At least, that was what she gathered from the fact that nobody at the university was allowed to speak about him.

On the day of her first appointment, Mara wandered the entire grounds looking for him. Nobody seemed to know where he lived, or even who he was. They must have taken a vow of silence about the matter, she thought.

But Mara was persistent, and soon ruled out all locales except the dilapidated obelisk. When she pushed away the vines and revealed a door, she knew this must be it. And, indeed, there was the Ori. He already knew who she was, and that she was sent by Aphrael, the priestess, to learn about the nature of reality.

For the past couple of months, since the start of the planting season, Mara had met with the Ori once a week. Each week he had given her a new problem, and discussed his disappointment in her failure to solve the previous.

Mara wasn’t inclined to give up. For the tenth time she pounded on the heavy door. Little bits of mortar rained down onto her hair as she pushed the door open and stepped inside with cautious confidence.

“Have you solved your problem?” the Ori asked, as he always greeted her.

She returned her usual greeting in reply, “No.” Her confidence fluttered out the window and joined the birds flying above.

“I see,” the Ori said, diverting his gaze for a moment.

“Do not be disappointed, Ori,” Mara exclaimed. “I tried. I really tried.”

The Ori nodded. “But if you wish to hold the world, open it up and see inside, you need to learn more than how to fish at the end of it.”

“Oh, I do want to hold the world,” Mara said. “See it all. That’s why I work. Hard. But, you see… please don’t be disappointed.”

“I think that if you want to understand the world, we would be best starting with yourself.”

“But I know my own self!” Mara exclaimed.

The Ori drew out a long hum as he stroked his beard. He had a penchant for prolonging his response just long enough to make Mara nervous. As soon as he saw her eyes look away, he replied, “Do you?”

“Oh, yes. See, I saw my image in the mirror, and immediately didn’t confuse me with my reflection.”

The Ori continued to hum, and after a moment Mara felt compelled to explain further. “Most people look in the mirror and see themselves. I look in the mirror and see another Mara who may look like me, but is much less creative and far more annoying in her way of always copying my actions.”

“That would be irritating, yes,” the Ori said. “However, I feel that you do not know yourself as well as you say you do.”

Mara shook her head. “Oh no, no, no. I know myself very well. Much more than my place in the world, it seems.”

“Well, then let us find out,” the Ori said. “One can hardly determine their place in the world if they don’t know how much of it they are occupying.”

“I don’t see how myself matters at all.”

“It matters all too much,” the Ori said. “If you wish to create a true model of the world, it must include yourself. Should it not?”

“Well, I don’t think I take up too much,” Mara said. “I demand very little, if anything at all – hardly any food or drink, and I never throw perfectly good things to waste.”

The Ori stroked his beard some more, and Mara grew very worried. He smiled. “How big are you? Do you know?”

“Yes,” Mara said. “I am 55 inches tall. And, I gather, 14 inches wide and 7 inches deep.”

“Then let us assume an ellipsoid Mara.”

Mara gasped. She crossed her arms in front of her chest and lowered her gaze. “Are you suggesting I have the build of an egg?”

“My dear,” the Ori said. “Just for ease in the calculation. It is only in the spirit of efficient mathematics.”

“Fine, so be it,” Mara said, “I see mathematics and flattery do not make good bedfellows.”

Peanuts (the best indigenous course to expand processing of nitric oxide!) In spite of what their name means, peanuts are not accurate nuts but a part of the vegetable family, and are identified with peas, lentils, chickpeas and different beans. viagra professional for sale You need Read Full Article free tadalafil sample to practice kegel exercises and yoga regularly. She qualified as viagra pills canada a herbalist 30 years ago and is a highly experienced medical professional. One can get this condition in inheritance click to find out buy generic viagra or due to excessive smoking.

“And you say you wish to be holding a little world. Suppose it’s ten percent the size of you, and on this world is another Mara of size ten percent of it.”

Mara nodded, humming away as she pretended to be in contemplation and not annoyance.

The Ori continued, “And, of course, the little Mara is holding another little world, with similar proportions, and it’s own little Mara, and so on and so forth.”

“Oh! Infinite me’s,” Mara laughed with elation. “Each one of them a darling and not at all egg-shaped.”

“Yes,” the Ori said, and smiled gently with only a hint of deviousness. “So, tell me, darling, what percent of this universe is Mara?”

“Oh, this should not do wonders for my ego, for I know the number will not be that much bigger than my presence in this room, so small all the same.” Mara stared at the ceiling while she thought. “But it shall be easy to compute. All I need to know are the dimensions of the room, of course.”

“Not so much,” the Ori said. “Because a true model of the world includes you, there’s no reason to believe that you’re not on another iteration of the model, with a bigger Mara watching you on a similarly proportioned sphere. And an even bigger Mara watching her, and so on and so forth upward as well.”

“Oh, I do not think I like this anymore,” Mara said as she bit her lip. “A bigger me would certainly have a bigger ego, and I shall fear I’d crush me like a bug out of the frustration of not knowing the answer.”

The Ori nodded solemnly, then smiled. “Then you best be off working on the solution. I much prefer for myself to be in three dimensions and not reduced to two, should you crush the world.”

 

{ Beat Mara to the solution! }

 

 

A Snippet of the History of Mathematics and Fiction

 

As mentioned at the start, this story was an experiment. It was mostly inspired by Lewis Carroll’s A Tangled Tale. Most people know Carroll for Alice in Wonderland – so A Tangled Tale seems to take the backseat in discussions of his work. The tale was a serial work, published in a magazine between 1880 and 1885. Each installment, called a knot, presented some number of mathematical problems.

Because A Tangled Tale was published in installments, Carroll would also discuss reader answers to the questions posed in the previous story.

Carroll was also known for the ribbing of readers who submitted incorrect answers, which was not always appreciated.

A Tangled Tale wasn’t the only such work attempting to combine mathematics and humor. A couple more examples would be Sideways Arithmetic from Wayside School, a spin-off of the Wayside series by Louis Sachar; and Dude, Can You Count? by Christian Constanda.

The latter two examples were published as books. A Tangled Tale was unique in that it included the dialogue between Carroll and the original readers. The entire text (the tale, and discussions) is available on Project Gutenberg.

As for the monthly riddles, here is a great opportunity to experiment a bit with the format of A Tangled Tale.

Each “riddle” presents a problem or two. At the end, the reader is invited to submit a solution before Mara does.

Speaking of solutions…

 

Solution to the June 2013 Riddle

 

If you haven’t worked out the solution to the June 2013 riddle for yourself, this is your last chance!

Seriously.

Once you read the answer, you can never solve it on your own… which, I may add, is an immensely satisfying feeling.

Of course, you could just argue with me over my solution, or how I worded the question. Depending on your personality, this may be just as fun.

 

Solution

The ages of the three children are 6, 6, 1.

 

Explanation

Textbook questions tend to give the student exactly what information they need to solve the problem… which I believe is poor preparation for the real world. But, I digress. There is just enough information in the narrative to solve the puzzle, and not a drop more.

The trick is rather devious. And it lies with the seemingly useless information that the mathematician gives his friend. The information itself isn’t useful (immediately), but the fact that it was needed does shed some light on the puzzle.

The product of the ages is 36. If you write all the ways you can multiply three numbers (positive integers, for those of you inclined to nitpick) to arrive at 36, you’ll find that most of the triples add up to a unique sum.

For example, 3, 3, 4 multiply to 36. These numbers also add up to 10. In fact, it is the only set of three positive integers that add to 10. If these were the ages of the children, the friend wouldn’t have needed the extra piece of information.

And this is the rub. There are only two sets of three positive integers that share the same sum: 6, 6, 1 and 9, 2, 2. The solution has to be one of these sets, because otherwise the friend would have been able to solve the problem without additional help. (Remember, he can see the number of windows).

Once you figure that out, the extra information itself is useful. 9, 2, 2 can’t be right, because there isn’t a “youngest child.” There are two “youngest children.” This means the correct answer is 6, 6, 1.

 

Winners List

 

No correct solutions were submitted – but thanks to everyone who submitted an answer.