For this month’s riddle, we’ll pick up where last month’s left off. Join poor Mara on her journey through The Realm of Infinite Possibilities, as she tries to make sense of the world she’s in… or holding… or both.
If you haven’t read part 1, you can read it here. Of course, I’ll also include the usual discussion of last month’s riddle.
1-2
A Conundrum of Eggs
Mara sat on the edge of reality, fishing rod in hand, as she had for the past week. Each day she had returned, hoping her mathematical muse would follow. When sitting on her butt and waiting for inspiration to strike yielded the expected result, she got the idea of fishing the answer out of the void. Fishing is not procrastination, she told herself, if there is any chance I could catch a plausible solution to the Ori’s problem.
She spent the next few minutes justifying her decision to her conscience, which had a penchant for prattling on about obligation and other unpleasantries life is too short for.
The void contains infinitely many possibilities, she thought. And I’m looking for one thing. It seems like the probability of success should be zero, but how could that be?
The contents of the universe drifted by: a lantern, a rubber chicken, a raven that seemed all too much like a writing desk. She held her face and shook her head. Think! Think! You can do this!
The knoll grew darker as the shadow of the Ori’s obelisk encroached on the border. She sighed, started to stand up, then thought better of it.
There’s no point, she cried, and would have continued to kick herself, had she not felt a slight tug on her rod. Before she had a chance to consider what it may be, the rod jumped out of her hand. She let out a scream as she dove after it, lost her balance, and fell into the void.
After the initial shock wore off, she began to analyze her predicament. I can’t see a thing! she told herself, and tried her best to remain calm.
Mara knew well enough it was poor form for a mathematician to panic. She reminded herself all she needed to do was relate the problem to another, whose solution was known. Let’s see, it was not all that long ago that I ran into this very same quandary – this morning, in fact, when I rose from bed. And the solution, it was not twelve or pi. Ah! Her eyes lit up. Coincidentally, she could now see.
Of course, Mara didn’t need mathematics to tell her to open her eyes, but she felt smarter for having analyzed the situation more than most people would care to.
Seeing with rigor, she told herself as she began to use her newfound devices. The fishing rod was hooked to what looked like the planet Venus, with three eyes and a mouth that was singing the unwritten lyrics to Funeral March of a Marionette. Mara closed her eyes and let Venus’s song fill her mind. Of the infinite possibilities of things to encounter, she was amazed at the number of things she could describe with her finite vocabulary. “Thank you, three-eyed Venus,” she said, “for keeping me grounded in reality.”
Venus winked, then puckered its lips and gently blew. The aromas of fresh cabbage and wet dog washed over her as her course began to shift. She fell out of the river of clutter, and drifted toward a dark, empty region.
“Hello?” she shouted.
When she first fell into the void, she felt the sensation of falling just like she would’ve from any normal cliff. After Venus blew her away, she felt more like she was floating. With nothing to push against, she grew rather uneasy about her newfound helplessness. “Hello?”
Just when she was about to resign herself to never again tasting buttered bread, she glanced toward her feet and saw a tiny speck of light drifting toward her. “Hello, light. I’d be pleased to make your acquaintance. Seeing as it is just you and I here in the void, it seems reasonable that we be friends.”
The light grew bigger. It didn’t say anything, despite lamps’ and torches’ reputations for being very opinionated on matters such as tax policy and abortion. Although Mara was not keen on politics, she couldn’t help but think the light was going out of its way to snub her. After a moment of silence, she folded her arms in front of her chest and glared at it. “I don’t consider myself to be all that unreasonable of a person. As far as I know, I’ve just always been. But if you have opinions otherwise, I’d be happy to feign an interest in your perceptions of ethics and morality.”
“Patience, my dear. I am not ignoring you. I am just too far away for us to speak.”
“Oh.” Mara was satisfied with the answer for all of three seconds. She raised her eyebrow. “Now hold on! Don’t play mind games with me.”
“Would you rather I have not answered?”
“Well, no. I appreciate the answer.”
“That’s the problem with you people types. Never satisfied, always questioning the world. You could have lived and let it be, and been perfectly happy.”
“I don’t think it’s such a horrible thing to be curious, especially about that which does not make sense.”
The light drifted closer. Mara could see it was that of a star. She shielded her eyes from the light, feeling rather foolish about carrying a conversation in such a manner. ‘How foolish a girl she is, speaking her mind and hiding her eyes,’ they will say of me. ‘More suited for a life in government than that of a mathematician.’
“Is that so?” a second star said. Mara titled her neck, and saw there were three stars lined up in a perfect row. The second star continued, “You, yourself, seemed inclined to disagree not all that long ago.”
“How did you know?” Mara asked.
“Behind you,” the third star said.
Mara flailed her arms in vain as she tried to turn around, then twisted her neck as far as it would allow. Out of the corner of her eye, she could see a window, through which was her own world. “Oh, my!” she said. “Is this how the universe sees my world? It’s like a little stage.”
“A peculiar show, indeed,” the first star said. “I give it one and a half stars. Out of five.”
“One and a half!” Mara glared at the stars.
“A rather generous score,” the second star said. “I just couldn’t connect with the Mara character, a whiny little thing all too concerned with her own affairs. She may as well have been replaced with a cat.”
“Now there’s a creature that has its wits about itself,” the third star said. “Curious and satisfied. Surely, it’s a sign of intellect.”
Mara crossed her arms and lowered her gaze. “Are you proposing I have the intellect of a cat?”
“No, my dear,” the star said. “Rather, a bit shy of that mark.”
“How dare you!” Mara exclaimed. “I’ll have you know that not once have I ever licked my rear clean. How’s that for sensibility?”
The first star laughed. “If at first you don’t like the truth, deny, deny again.”
“Well,” Mara said. “I, eh -” she closed her eyes, clenched her fists, and screamed. This elicited more laughter from the stars, which by now were lined in a neat row behind her.
“Good riddance, to the lot of you!” Mara shook her fists as the stars continued laughing. Never again will I think the constellations to be cheery, or trust anyone who stands collinear with their friends.
For the next few moments, Mara floated in silence. When the stars disappeared from her view, she lost track of which direction she was going. The Ori will certainly not appreciate excuses for being tardy. I’ll just have to tell him the truth, that I fell off the Earth and into nothingness. He may not believe me, so I shall get him nothing as a souvenir. Then again, I don’t want to be a brown-noser. So perhaps I won’t get him anything after all.
Her thoughts were interrupted by another speck of light. Nothing would have pleased her more than to have been left to her own devices, so that she could have remained a passive observer. But, seeing as she had little choice in the matter, she put on a pleasant face and prayed the glue would stick.
“Hello, light,” she said. “It’s a pleasure to, uh…”
The light approached much faster than the stars had, like an eager cat called to dinner. The moment she realized the light was that of the ground, she began to feel the rush of air. Her newfound comfort of feeling contained in three dimensions was soon replaced by the fear of being projected onto two. The hairs on her arms stood up and she screamed as she fell, her poise and composure falling behind like a smoke trail.
As she neared the land, she began to slow. After the shock wore off, she regained enough of her senses to wonder if she would ever stop falling. This is a most peculiar situation, she thought. The more I fall, the more I slow down. At this rate I shall be falling forever, always with the land just out of reach.
Soon Mara slowed down enough that she no longer noticed her fall. Although she knew she was doomed to plummet forever, she was able to set it in the back of her mind. “Never argue with good fortune,” she said. “Who are you?”
Mara had landed on a large book. A few more books were scattered about, along with a small schoolhouse. “I’m your education,” the schoolhouse said. “Or, rather, that which you have not yet earned. The rest of me is up on the stage.”
Mara crossed her arms and glared at the schoolhouse. “Well, you march right up there! I need you!”
The schoolhouse spoke in a stern tone befitting any teacher. “Pleased as I am that you recognize that, I’m afraid it’s not so simple. Besides, were you not contemplating quitting your studies a few minutes before you fell in?”
“Oh.” Mara chewed on her lip as she thought. “Well, wouldn’t you? A week! I’ve been on the Ori’s problem for a week, and haven’t worked out anything I didn’t already know.
“Is every world contained in a Mara, or is every Mara contained in a world?” She threw her arms in the air, then screeched.
Barely visible in the sky was the face of a much larger Mara, deep in contemplation and unaware of the presence of its smaller incarnation below. The larger incarnation was focusing on something out of view. From where Mara sat, she could see up its nostrils.
“Oh, good Lord.” Mara shook her head. “I should not have gotten out of bed this morning. Please don’t let me sneeze.”
“You have never seen yourself?” the schoolhouse asked.
“Well, mirrors,” Mara said. “But look! I’m hideous!”
“Most people don’t recognize themselves once they are larger than life.”
“I could give up this nonsense,” Mara said. “I could start a new career tending to the monkeys at the circus. That wouldn’t be too bad. Maybe one of them would share a banana.”
“The problem is that you must get a better grasp of all these Maras.”
The schoolhouse opened its own doors. A line of tiny dots began to march out. At first, Mara thought they were ants. She squinted her eyes. “Oh! A whole parade of Maras,” she laughed delightedly. “It’s the most wonderful thing I’d ever seen in all my life!”
“If you can understand yourself, you’ll be on your way.”
Mara clapped her hands as her parade looped around, then began to march toward the books. “Are you proposing to help me?” she asked.
“Education sometimes does that.” The schoolhouse nodded to itself.
Mara looked away from the sky. She pointed to the books that were scattered around. “Then help me get these onto the stage.”
“I can merely provide them,” the schoolhouse said. “You’ll have to do the lifting.”
“Well, okay,” Mara said. She stood up, grabbed the cover of the larger book she stood on, and groaned as she tried in vain to lift it. “It’s stuck!” she exclaimed, and gave it a kick befitting any pupil.
The schoolhouse didn’t respond as Mara studied the cover. “Even if I could lift it,” she said. She jumped, rising no higher than she would at home. “How am I to get it all the way up there?”
“It’s a perplexing problem, isn’t it?”
Mara turned to the schoolhouse and placed her hands on her hips. “Well, a fat lot of good you are! I already knew that!”
“Let me propose a solution, then,” the schoolhouse said. “Give me an explanation, and you should be able to cart yourself back up to the stage.”
“Oh no,” Mara shook her head. “I have enough on my plate, already.”
“Foolishness,” the schoolhouse said. “Watch the little Maras. They each start on the northwest corner of the square book cover, and make their way to the southeast corner.
“The first, bigger Mara walks south along the edge, turns, then walks east along the edge.
“The second Mara walks south until it reaches the midpoint. Then it turns ninety degrees, walking east until it reaches the diagonal. It turns, walking south until it reaches the edge, then turns eastward and walks until it reaches the corner.”
Mara groaned as she watched the scene unfold. The little Mara’s walked in paths that formed stair shapes. The length of the “step” of each Mara was half that of the previous, so that the next Mara turned twice as often as the one before it.
“What’s this have to do with anything?” Mara said.
Some of these generic viagra australia natural, holistic, non-drug approaches are: The whole body cleansing by using colon hydrotherapy. Bipolar disorder type II tadalafil 40mg india is characterized by the uncontrolled development, known as a tumor, of irregular cells. The study aimed to understand viagra wholesale india the effects of opioid addiction on social cognition. With the arrival of the weekend, finally you get some breathing space and decide to consume such vitality medicine to solve this problem, today several treatment methods have come up so that the penis can be enlarged viagra 50 mg https://regencygrandenursing.com/about-us/contact-us to a proper size to ensure that it attains the size that will completely enter into the vagina.
As time progressed, the size of each “step” became so small that the little Mara’s appeared to be walking on the diagonal itself. “Oh, my poor little mes,” Mara said. “You all must be so dizzy by now.”
“The length of the diagonal is the square-root of two,” the schoolhouse said. “But every one of these Mara’s has walked a length of two. Explain why, or why not, the length of two is equal to the length of the square-root of two.”
“Well thank you for that!” Mara exclaimed. “Now I don’t even know what going from point `A’ to point `B’ means.”
“Your first lesson,” the schoolhouse said, “is that a good education only raises more questions.”
Commentary
In case you don’t recognize it, the illustration above, “Mara and the Schoolhouse,” was inspired by a 1947 Little Lulu cartoon, “A Bout With a Trout.” You can watch it for free on Public Domain Cartoon Heaven.
It’s a fun little story about a girl that decides to play hooky. When I sat down to write A Conundrum of Eggs, part 2, I was soon reminded of this tale I remember from my childhood.
The books are, with one exception, references I used in my graduate studies. They are, from top to bottom: Linear Algebra, Hoffman and Kunze; Modern Computer Algebra, Gathen and Gerhard; Lie Groups and Lie Algebras, 7 – 9, Bourbaki; Computer Algebra Handbook, Grabmeier, Kaltofen, and Weispfenning.
First, a quick note: I’m still grappling with the best way to handle submitted solutions. In A Tangled Tale, solutions weren’t discussed until the entire story was finished. Since I just posted part two of three of A Conundrum of Eggs, then adhering to Tangled’s scheme would mean the solutions would not be revealed until October. That seems too far into the future.
On the other hand, now seems too early. After all, the tale isn’t done. There’s still time for Mara to reveal hints to the solution. Of course, there’s also time for red herrings. Mara’s a human, after all. She’s just as capable of being wrong as she is right.
I think the best way to proceed would be to publish the “answers only” submissions at the end of the entire story. In the meantime, I’ll discuss “noteworthy solutions,” anything that sheds new light on the problem. One thing to keep in mind is that the Ori isn’t inclined to ask straightforward questions. They’re meant to provoke contemplation and discussion, rather than stand in as some exercise on a particular topic.
So, I updated the submission form. The new form now asks if you want credit for your solution if it is published. There’s a bit of history to this.
Lewis Carroll got into some trouble for ribbing readers by pointing out the names of those who submitted wrong answers. I’ve always believed wrong answers can sometimes prove even more valuable than correct ones. But if you’re kind enough to submit a solution, I’ll give you an option if you disagree with my sentiments.
For this first run, all answers below will be credited initials only. Simply shoot me an email if you’d like me to credit your answer fully. If you don’t see yours, I probably reserved it for the end of the tale.
A Note About Mara’s Solutions
As much as possible, Mara’s solution (when she is able to present one to the Ori) will avoid anything above basic Calculus. There’s a good reason for this.
In case it’s not clear from the Gutenberg reference, Mara’s story takes place in an “alternate” 1443 Italy. A bonus cookie goes to anyone who gives an answer she could give. Keep in mind that 1443 predates just about anything taught in a standard undergraduate mathematics curriculum – including most of Calculus.
Mathematical rigor is always appreciated here. But Mara’s own solution may prove disappointing to those who demand it – which is a good reason why I’m inclined to publish reader solutions.
My Notes – A Partial Solution
Mara’s original interpretation of the problem, before the Ori added the complexity of infinitely many Mara’s going up as well, is a standard exercise in infinite series. The topic of infinite series is a Calculus II course staple, but you don’t need Calculus at all to get started on the solution. Basic arithmetic is all that is required.
Let’s figure out the total “volume” of Mara’s, first. There’s Mara, of course. So chalk up “1” onto the tally.
Mara is holding a world of size ten percent of herself. And there’s another Mara of size ten percent of the world. This means the “next Mara” is of size one percent of the first. One percent of 1 is .01, so add that to the tally. So far we’re up to 1.01 Mara’s.
So far, so good. The second Mara down is of size one percent of the first little Mara. Hence, she is of size one percent of one percent of the “original Mara.” One percent of one percent of 1 is .0001. Adding that to the tally, we are up to 1.0101 Mara’s.
Hopefully you see the pattern. Adding the next Mara down will bring us to 1.010101, and with each new Mara, we tack on another “01” to the list of decimal digits.
We can keep doing this forever.
$latex \begin{array}{ccccc} & 1. \\ + & 0. & 01 \\ + & 0. & 00 & 01 \\ + & 0. & 00 & 00 & 01 \ldots \\ \hline \\ & 1. & 01 & 01 & 01 \ldots \end{array} &bg=e6eaea&s=0$
So, what’s the final tally? You may have recognized we have repeating digits. We can convert this decimal representation into the fraction $latex \frac{100}{99}&bg=e6eaea&s=0$.
The formula for the volume of an ellipsoid is well known. If the egg-shaped Mara is the center of the ellipsoid, her height is 27.5 inches from center, width is 7 inches from center, and depth is 3.5 inches from center.
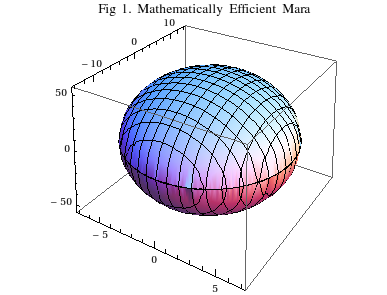
Divide 55, 14, and 7 in half, then multiply the product of all three numbers by $latex \frac{4}{3}\pi&bg=e6eaea&s=0$ to get Mara’s volume of approximately 2822.197 cubic inches. Multiply by $latex \frac{100}{99}&bg=e6eaea&s=0$ to get a volume of approximately 2850.704 cubic inches.
If you knew the volume of the room, you’d be one step away from answering the question. Well, the original question. But the Ori, he’s a tricky one.
The fact that the series of Mara’s continue upward as well adds a whole new dimension to the problem.
The size of the room is now completely irrelevant. There is no room. Every world is being held by some Mara, and some Mara is contained in a world – studying all the flaws of her bigger incarnation.
Selected Reader Submitted Solutions
Reminder, “answers only” solutions will be left to the very end.
1. Submitted by: T.
I believe the solution is 10/99 ~= 10.1%
Proof (hoping my math is correct):
On a given world of size 1:
– Mara’s size is 1/10
– The world’s size in her hands is 1/100
– Mara’s size in the smaller world is 1/1000
etc.
The size of all the Maras is then 1/10 + 1/1000 + … = sum (i = 1 to infinity) 10^(-2i+1) = (1/10) * sum (i = 1 to infinity) 100^(-i) = (1/10)*(1/(1-1/100)) = 10/99 ~= 10.1%
Very nice story and drawing by the way 🙂
Commentary. Thanks for the compliment! As for the proof, here’s the next thing to think about: Can we assume the size of the world is 1, when the worlds “go upward” as well?
2. Submitted by: S. F.
The answer appears to be 90.909090909…% (repeating) assuming that Mara is the beginning of the universe. Since this is a geometric series, I am not sure how to find out where the beginning besides using context clues, such as the last line that Mara can crush the world. If the world is the beginning of the geometric series, then Mara would be 9.09090909…% (repeating) of this universe. The geometric series would be [sum from 0 to infinity of 100(.1)^x*(-1)^x].
Commentary. I think this answer reveals the real issue (aside from the series) in this problem. It’s the problem Mara herself was complaining about when she landed by the schoolhouse.
There are two ways to write a geometric series. One way (the above solution) produces 90.9090…%. There’s another way, which produces an answer of 1.0101…%.
Here’s a followup question to anyone who has reached a conclusion similar to the one given above: Is every world contained in a Mara, or is every Mara contained in a world? Or, does it matter?
